A Brief Survey on Material Models for Finite Element Simulations of Deep Tunnels
Tassilo Weifner*
Brenner Base Tunnel BBT SE, Innsbruck, Austria
*Corresponding author: Tassilo Weifner, Brenner Base Tunnel BBT SE, Innsbruck, Austria
Article History
Received: February 04, 2020 Accepted: February 09, 2021 Published: February 11, 2021
Citation: Weifner T. A Brief Survey on Material Models for Finite Element Simulations of Deep Tunnels. Int J. Res. Case Rept & Case Sers. 2021;1(1):05‒07. DOI: 10.51626/ijcrs.2021.01.00002
Abstract
In finite element simulations of deep tunnels an appropriate selection of a suitable material model is of crucial importance. Oftenly, quite simple material models as the Mohr-Coulomb model [1] or even the Drucker-Pager model [2] are used for finite element calculations of deep tunnels. In the contribution the shortcomings of these models will be explained and the requirements for material models for deep tunnels are discussed. Some more complex material models are presented, which were developed in the last decades.
Mini Review
We speak of deep tunnels if the overburden height is much larger than the other dimensions of the model and therefore it is not possible or useful to model the whole soil or rock mass located above the tunnel. Moreover, the variation of the overburden stress level in the zone of the tunnel is insignificant compared to the amount of the overburden stress and therefore the stress level can be assumed to be constant [3]. However, during the excavation process of the tunnel, the stress level of the confining soil/rock can vary significantly and therefore material laws, which can cope with different stress levels are necessary.
Elasto-Plastic Models (Hyperplasticity)
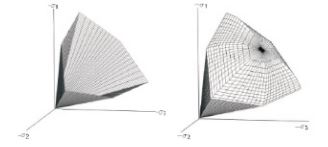
In elasto-plastic constitutive models (also called hyperplastic models) the material behaviour is ‘switched’ between elastic and plastic behaviour. This switching is made with the aid of pre-defined surfaces, one or more yield surface(s) and eventually a cap (‘cap models’). In Figure 1 can be observed on the left the yield surface of the Mohr-Coulomb constitutive model and on the right the yield surface and the cap of the Hardening Soil model.
Figure 1: a) Yield surface in stress space (left) and b) Yield surface and cap (right).
Cam-Clay model
This model is the first critical state model for describing the behaviour of soft soils such as clay and was developed at the University of Cambridge in the sixties of the last century [4]. It combines the critical state theory with elastoplastic concepts. The soil behaves elastically until the yield surface is reached, thereafter in addition to elastic strains εc also plastic deformations (corresponding to εp) occur. Considering the stress-strain behaviour after reaching the yield surface, the stress can remain constant, increase or decrease. In the first case the behaviour is called elastic perfectly-plastic. In the Cam-clay model, however, are possible only the second and the third cases which are called strain hardening and strain softening, respectively.
The first model was developed in Cambridge and is called the (original) Cam-Clay model (SCHOFIELD and WROTH) [4], later appeared the Modified Cam-Clay model (BURLAND and ROSCOE) [5] which differs with respect to the shape of the yield locus: the first uses a part of a logarithmic spiral, the second an ellipse. A disadvantage of the yield locus in the original Cam-clay model is the lack of smoothness in the apex, which can cause numerical problems. The models use in the stress space a conical failure surface whose projection in the deviatoric plane is a circle (cf. Drucker-Prager model [2], explained in the following section). This shortcoming leads to unrealistic shear strength for some stress paths (e.g. triaxial extension).
The Cam-Clay and Modified Cam-Clay models may allow for unrealistically large ratios of shear stress over mean stress when the stress state is above the critical state line. Furthermore, these models predict a softening behaviour for the state of stress on the dry side of the yield surface [6]. Without special considerations, the softening behaviour leads to mesh dependency of a finite element analysis. The use of these two models in simulations of practical applications including general boundary valued problems is not recommended.
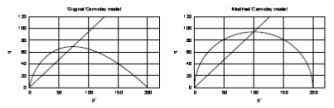
Figure 2: Section in the p’-q plane of cap and yield surface (critical state line)
a) Original Cam-Clay model (left) and b) Modified Cam-Clay model (right).
Drucker-Prager model
The Drucker−Prager model was proposed by Drucker and Prager (1952) [2] to describe the stress–strain behavior of pressure-dependent materials such as soil, rock, and concrete. The model uses in the stress space a conical failure surface whose projection in the deviatoric plane is a circle. This shortcoming leads to unrealistic shear strength for some stress paths (e.g. triaxial extension) and is therefore not recommended in simulations of practical applications, especially in tunnelling, where during the excavation in the extension stress path the shear strength is underestimated.
Mohr-Coulomb model
Soils behave rather non-linear when subjected to changes of stress or strain. In reality, the stiffness of soil depends at least on the stress level, the stress path and the strain level. The Mohr-Coulomb model [1] however, is a simple and well-known linear elastic perfectly plastic model, which can be used as a first approximation of soil behaviour. The linear elastic part of the Mohr-Coulomb model is based oin Hooke’s law of isotropic elasticity. The perfectly plastic part is based on tlhe Mohr-Coulomb failure criterion, formulated in a non-associated plasticity framework.
A perfectly-plastic model is a constitutive model with a fixed yield surface, i.e. a yield surface that is fully defined by model parameters and not affected by (plastic) straining. For stress states represented by points within the yield surface, the behaviour is purely elastic and all strains are reversible. The yield surface used in the Mohr-Coulomb model is –different to the Cam-Clay model and the Drucker-Prager model– not circular and the shear strengths for different stress paths are compatible with the real soil behaviour. This material law is therefore in accordance with the geotechnical standards.
Hardening-Soil model
The Hardening-Soil model [7] is an advanced model for the simulation of soil behavior. As for the Mohr-Coulomb model, with the Hardening-Soil model limiting states of stress are described by means of the friction angle φ‘, cohesion c and the dilatancy angle ψ. However, soil stiffness is described much more accurately by using three different input stiffnesses: the triaxial stiffness E50, the triaxial unloading stiffness Eur and the oedometer loading stiffness Eoed. The hyperbolic equation of Kondner [8] is used for the description of the stess versus strain behavior in triaxial test conditions. In contrast to the Mohr-Coulomb model, the Hardening-Soil model also accounts for stress-dependency of stiffness moduli.
Hypoplasticity
In hypo plasticity different to elasto-plasticity no distinction between elastic and plastic behaviour is necessary. The assumption of elastic behaviour is not necessary; the material behaviour is plastic since the very beginning.
The first model was developed by KOLYMBAS [9]. Later developments were done by VON WOLFFERSDORFF [11] for non-cohesive materials and by WU [10] for rocks.
Hypoplastic model for clay and sand
In 2006 was developed a model for cohesive and non-cohesive materials [12]. It can model the behaviour of clay with the same set of material parameters for several states of consolidation. Barotropy (stress dependent behaviour) and psychotropy (density dependent behaviour) can be successfully modelled.
Due to the properties afore mentioned, especially the possibility to model stress dependent stiffness, the model appears to be suitable to simulate deep tunnels. The hypoplastic model used here has the advantage different to the often used hypo-plastic model of von Wolffers dorff [11]– that in its formulation no limits of void ratios (which play a limited role for rocks) are used, which make the present model suitable for the simulation of isotropic rock.
Conclusions
The proposed models (Mohr-Coulomb model, Hardening Soil model and hypoplastic model) were used for finite element simulations for the Brenner Base Tunnel. The Brenner Base Tunnel (BBT) will be the world’s longest tunnel with a total length of 64 km and will connect as a railway tunnel Innsbruck (Austria) with Fortezza-Franzensfeste (Italy). The Brenner Base Tunnel is composed of two parallel main tunnels with a diameter of 9m and a distance of 70 m and a smaller emergency tunnel in between the two main tunnels, situated 12m below. The system includes also three underground emergency stations, two connection tunnels to the existing Innsbruck railway bypass tunnel and also rescue and access tunnels. The proposed model could be used successfully to simulate many of the interactions between the numerous tunnel drives [13-16].
References
- Mohr O (1914) Abhandlungen aus dem Gebiete der Technischen Mechanik. Ernst und Sohn.
- Drucker DC, Prager W (1952) Soil mechanics and plasticity analysis or limit design. Quarterly of Applied Mathematics 10: 157.
- Kolymbas D (2008) Tunnelling and Tunnel Mechanics. A Rational Approach to Tunnelling. Springer, Berlin, Germany.
- Schofield AN, Wroth CP (1968) Critical State Soil Mechanics, McGraw-Hill, pp. 310.
- KH Roscoe, JB Burland (1968) On the generalised stress-strain behaviour of ’wet’ clay. In J. Heyman and F. Leckie, editors, Engineering Plasticity, Cambridge University Press, pp. 535-609.
- Weifner T (2006) Review and Extensions of Hypoplastic Equations, Advances in Geotechnical Engineering and Tunneling, Logos Verlag, Berlin.
- Schanz T, Vermeer PA, Bonnier PG (1999) The Hardening Soil model: Formulation and verification. Beyond 2000 in Computational Geotechnics – 10 Years of PLAXIS. Rotterdam: Balkema, pp. 281-296.
- Kondner RL (1963) Hyperbolic stress-strain response: cohesive soils. Journal of Soil Mechanics & Foundation Eng., ASCE, 89(SM1): 115-141.
- Kolymbas D (1988) Eine konstitutive Theorie für Böden und andere körnige Stoffe. Publ. series of: Institut für Bodenmechanik und Felsmechanik der Universität Fridericiana in Karlsruhe, No. 109.
- Wu W, Huang W (2000) Rational approach to anisotropy of rocks. In Proc. EUROCK Symposium, 2000, pp. 623-628.
- von Wolffersdorff A (1996) A hypoplastic relation for granular materials with a predefined limit state surface, Mech Cohesive Frict Mater 1: 251-271.
- Weifner T, Kolymbas D (2007) A hypoplastic model for clay and sand, Acta Geotechnica 2: 103-112.
- Weifner T, Unteregger D, Bergmeister K (2017) Macro Scale Numerical Modelling for the World’s Longest Tunnel. World Engineering Forum 2017, Rome, Italy.
- Bergmeister K, Weifner T (2019) Learning from Complexity – Geomechanical Back Analysis of Complex Rock Failures of the Brenner Base Tunnel. Sustainable Industrial Processing Summit & Exhibition, Paphos, Cyprus.
- Cordes T, Weifner T, Unteregger D, Bergmeister K (2019) Interaction between Deep Tunnel Drives and Existing Tunnel in Fault Zones –Modelling Against Reality. Geomechanics und Tunneling 12(6): 641-650.
- Weifner T, Bergmeister K (2019) 3D Simulations for the Brenner Base Tunnel Considering Interaction Effects. ITA-AITES World Tunnel Congress 2019, Naples, Italy.