International Journal on Engineering Technologies and Informatics (IJETI)

Mini Review Volume2-Issue3

Homeostasis and Homeorhesis: Sustaining Order and Normalcy in Human-Engineered Complex Systems

Asok Ray*

Department of Mechanical Engineering and Department of Mathematics, Pennsylvania State University, USA

*Corresponding author: Asok Ray, Department of Mechanical Engineering and Department of Mathematics, Pennsylvania State University, University Park, USA
Article History
Received: May 28, 2021 Accepted: June 15, 2021 Published: June 18, 2021
Citation: Ray A. Homeostasis and Homeorhesis: Sustaining Order and Normalcy in Human-Engineered Complex Systems. Int J Eng Tech & Inf. 2021;2(3):63‒65. DOI: 10.51626/ijeti.2021.02.00014

Download PDF

Abstract

This letter explores the notions of biological homeostasis and homeorhesis for construction of hybrid decision & control laws for human-engineered complex systems, the complexity may remain dormant during normal operations, but it becomes acutely conspicuous when contributing to unanticipated cascading and pervasive failures. The objective here is to sustain order and normalcy under both anticipated and unanticipated anomalies, faults, and disturbances. As an example, macroscopic decision & control of material microstructures is presented.

Keywords: Human-engineered systems; Hybrid decision & control

Introduction

The integration of control, communications, and computation has spawned the development of human-engineered systems of bewildering complexity, comparable to that seen in biological systems [1]. This complexity remains cryptic during normal operations, but it may become acutely conspicuous when contributed by unanticipated cascading of pervasive anomalies and faults, leading to catastrophic failures like the August 2003 blackout in the power grid of North America. In general, complexity emerges as a consequence of uncertain nonlinear dynamics of the interacting components at multiple spatial and temporal scales, as the system behavior changes from strict order to chaotic. From these perspectives, the notions of biological homeostasis and homeorhesis [2] are explored here for construction of hybrid decision control laws for applications to human-engineered complex systems.

Homeostasis is the natural tendency of a living organism to maintain a stable equilibrium [3,4] in the thermodynamic sense [5] among its interacting internal components, regardless of their interactions with the external environment. For a dynamical system, homeostasis can be viewed as sustaining internal stability [6]. In contrast to homeostasis, homeorhesis [7, 8] is the natural tendency of a living organism to continue its evolving development, albeit being possibly different under diverse environmental conditions. In other words, homeorhesis is the property of dynamical systems to converge to a (possibly new) stable trajectory after being perturbed. Therefore, a combination of homeostasis and homeorhesis [2, 8] can be viewed as a tool for maintenance of order and normalcy in the state trajectory under internal anomalies & faults as well as under exogenous disturbances to avoid a potential chaos.

¹Walter Cannon introduced the term “homeostasis” in 1932 from two Greek words: ‘homeo’ meaning ‘similar’, and ‘stasis’ meaning ‘to remain the same’; together they mean ‘steady state’. The term “homeorhesis,” also derived from two Greek words meaning “similar flow”, was introduced by Clark Waddington around 1940.

Technical Concept

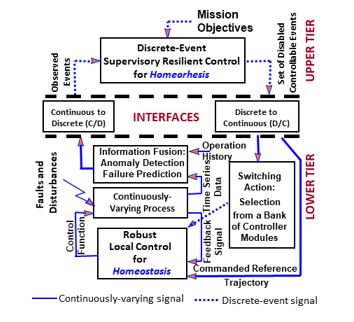
Usually human-engineered complex systems are hybrid [9,10] in the sense that continuously-varying physical processes (e.g., fluid flow and flexible structures) and the dynamics of discrete events (e.g., anomalies & faults, environmental disruptions, and human actions) interact with each other. The two-tier architecture in Figure 1 illustrates a concept of hybrid decision & control by following the notions of biological homeostasis and homeorhesis. While the robust local control at the lower tier sustains internal stability [6], discrete-event supervisory resilient control [9] at the upper tier attempts to maintain order and normalcy under component-level anomalies, faults, and exogenous disturbances, albeit with (possibly) gracefully degraded performance.

It follows from Figure 1 that the continuously-varying information, derived from time series data of observed macroscopic variables and process operation history, generates the events that are inputs to the supervisory controller, at the upper tier, which makes homeorhesic decisions on how the underlying process should be operated and what controller should be selected at the lower tier. For example, if the time series data of observables indicate potentially imminent instability, the supervisory decision would be to switch to a more conservative lower-tier controller at the expense of gracefully degraded performance; similarly, performance could be enhanced by safely switching to a more aggressive controller if the current control system is found to be robustly stable [6]. The switching algorithm at the lower tier must ensure smooth transfer from one controller to another whenever such actions are undertaken [11]. The supervisor may also choose to alter the reference trajectory, as seen in Figure 1, to sustain order and normalcy and to achieve high performance. Behavior pat- terns, derived from time series data of process observables, carry critical information on potentially pervasive anomalies and associated disorder [12]. Concepts borrowed from thermodynamics and statistical mechanics [5] have been used for analysis and synthesis of complex behavioral patterns in several disciplines such as biological sciences [1]. Specifically, thermodynamic analysis of multi-fractals has evolved as an important branch of nonlinear science [12,13], where complexity emerges from stochastic and nonlinear multi-scale spatio-temporal dynamics of the interacting components as the system starts evolving from ordered to chaotic conditions. As an example, macroscopic decision & control of material microstructures is presented in the next section.

Figure 1: Homeostasic and Homeorhesic Decision & Control.

Macroscopic Decision & Control of Microstructures

The microstructures of physical processes (e.g., evolutionary intelligent materials) are usually modeled to be sufficiently complex to capture the process characteristics, and their interactions with applied continuum fields form a challenging problem. For example, electric and magnetic fields may couple to other fields, such as strain, molar composition and temperature, and the associated field properties are spatially coupled to the microstructure through the respective constitutive equations. Such couplings are prevalent in a variety of materials, such as piezoelectric, electrostrictive, and magnetostrictive [14]. Small defects and inclusions in microstructures may drastically change the macroscopic behavior of materials. These phenomena are analogous to chaotic behavior in biological systems [1] and to phase transitions in thermodynamic systems [5,12]. The anomalies in the microstructures may be benign or malignant, similar to those in living organisms [1]. The concept is formulated so that com- plex microstructures can acquire the ability of self-diagnosis and self-healing through usage of diagnostic, prognostic, and therapeutic techniques that are analogous to those employed in medical practice in the following sense.

Similar to the notion of injecting medication or inoculation on a patient, a material microstructure could be stimulated with macroscopic control functions as inputs, such as dope injection, ultrasonic excitation, or temperature perturbation. Decisions on self-diagnosis, health monitoring, and healing need to be made as early as possible based on the real-time information, derived from the responses to these control functions. The inferred information on health status can then be used for self-healing.

The objective here is to elucidate how the concept of biological homeostasis and homeorhesis [2,8] can be gainfully utilized for decision & control of macroscopic behavior of material microstructures under various anticipated and unanticipated anomalies, faults, and exogenous disturbances.

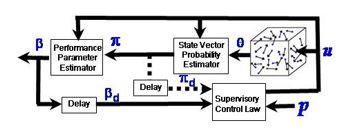
Nomenclature of Parameters in the Figure

performance specifications (p); macroscopic control function (u); performance hyper-parameter (þ) and its delayed value (þd); estimated state probability vector (u) and its delayed value (ud ); time series of observables (8)

Figure 2 conceptualizes a hybrid decision & control system for material microstructures, where the dynamics of macroscopic variables are significantly (e.g., several orders of magnitude) slower than those of the complex microstructures, as pictorially represented by random particles within the cubical box. This configuration follows the homeostasis and homeorhesis architecture in Figure 1 such that the closed loop system at the lower tier is represented by the cubical box in Figure 2, without showing the details of control and switching actions in the lower tier. The salient information from random process dynamics of microstructural particles at the cubical box can be captured by using the analytical (e.g., symbolic time series analysis tools (STSA) [15–17]) as explained below in view of Figure 2.

Figure 2: Schematic diagram for decision & control of the macroscopic behavior of material microstructures.

Given the time series data (8) of quasistationary response(s) of macroscopic observable(s), which are stimulated by the macroscopic control function (u), the (finite- dimensional) probability vector (u) of the canonical ensemble states is derived as the natural invariant density of the Perron-Frobenius operator or the Koopman operator (e.g., the dominant left eigenvector of the state transition matrix of the probabilistic finite state automata (PFSA) models of the microstructure behavior) [13]. In this context, based on a time series (휽), two tasks are defined as follows:

• Estimation of the hyper-parameter (휽) of performance variables (e.g., anomaly conditions, damage states, and state derivatives).
• Statistical control of the microstates via manipulation of macroscopically controllable function u so that the performance specifications (p) are satisfied.

The next step is to identify the hyper-parameter (휷) from the probability vector (흅) and the information on the macroscopic control function (u). The continuous hyper-parameter (휷) is analogous to intensities like the inverse temperature in the thermodynamic sense [5]. The key idea here is to extract the dynamic Renyi information [12] from the profile of 휷 at the slow time epochs of the macroscopic dynamics. The supervisory controller at the upper tier of Figure 1 is fed with the sequence of discrete events that are generated from the delayed information, 휷푑 and (possibly) 흅푑.

The “delay” in Figure 2 indicates that the information at the previous time epoch is used to (asynchronously) generate the current supervisory decision. The delay is expected to be non-uniform as it is dependent on both the process dynamics and evolution of faults and disturbances. In Figure 2, the macroscopic performance specifications p, as an input to the supervisor, represents the mission objectives in Figure 1.

Summary and Conclusion

This letter has presented an exposition of the notions of biological homeostasis and homeorhesis [2,8] to conceptualize system architectures for macroscopic (hybrid) decision & control of microstructural behavior dynamics in human-engineered complex systems. The objective here is to sustain order and normalcy in such dynamical systems (e.g., manufacturing of complex materials, fossil-fueled & nuclear-fueled power generation, and military command & control) under both anticipated and unanticipated anomalies, faults, and disturbances. As an example, a procedure is outlined to formulate decision & control system architectures for complex material microstructures. Further multidisciplinary research efforts are needed to fully realize the concept of the proposed architecture and subsequently synthesize the associated decision & control laws.

Acknowledgment

The reported work has been supported in part by U.S. Air Force Office of Scientific Research (AFOSR) under Grant No. FA9550-15-1-0400 in the area of dynamic data-driven application systems (DDDAS). Any opinions, findings, and conclusions in this paper are those of the author and do not necessarily reflect the views of the sponsoring agencies.

References

Homeostasis and Homeorhesis: Sustaining Order and Normalcy in Human-Engineered Complex Systems

Asok Ray*

ISSN: 2769-6146

IJETI Menu