Productivity Theory for Industrial Engineering
Ryspek Usubamatov*
Kyrgyz State Technical University I. Razzakov, Kyrgyzstan
*Corresponding author: Ryspek Usubamatov, Kyrgyz State Technical University I. Razzakov, Bishkek, Kyrgyzstan
Article History
Received: May 03, 2021 Accepted: May 06, 2021 Published: May 07, 2021
Citation: Usubamatov R. Productivity Theory for Industrial Engineering. Int J Eng Tech & Inf. 2021;2(2):31‒34. DOI: 10.51626/ijeti.2021.02.00009
Abstract
Engineering is solving the pivoted problems of the state economy that are the productivity of industry and the quality of the output product. The solution to these problems is seeing by the intensification of the technological process and its structural arrangements. The intensification of the technological process has limitations due to its physics of execution. The structural arrangements of the process are limited by the technical indices. Both limitations depend on numerous physical, technical, and economic constraints. Finding the optimal solution for the pivoted problems of the industry depends on the tactical and strategic goals of the production economics. Both goals depend on the marketing environment. The tactical goal of the production process is solving by the optimization of its technological process and structural arrangements by the criterion of the maximal productivity rate of the physical process. The strategic goal is solving by the optimization of its production process by the criterion of the minimal production cost. Productivity theory considers physical productivity and gives the solution for the tactical goals of industrial engineering.
Keywords: Productivity theory; Technological process and Structure; Optimization
Introduction
Beginning from Industrial Revolution scientist, researchers, engineers published tons of manuscripts dedicated to the problem how to increase the labour productivity, productivity rate of economic system, and quality of the products fabricated. Analysis of these publications demonstrate the partial and simplified solutions of industrial problems. It can be explained by the complexity of the problem that based on principles of different physical nature of production process that should be formulated by the complex mathematical expressions. For example, manufacturing processes are based on technology, production machine deign and system, reliability of them, system of maintaining, management, ergonomics, etc. Each of them today based on own theories which combining in one holistic theory was problematic for the long time [1,2].
During the centuries, manufacturing industries accumulated experience in creating different machines and complex systems for the production of various goods, work parts, and products. All these diversities of machines and systems with different designs are solving the pivoted problems of economics to increase the productivity rate of manufacturing processes with high-quality products [3,4]. Productivity rate for manufacturing systems is the primary area of any industry in the world. Manufacturers are interested in any publications that focused on the problem of solving productivity problems. Economists consider two types of economics, i.e., macro and microeconomics that related to the economics of the production system of companies and state industries or labour productivity respectively [5,6]. Macroeconomics operates with the term of productivity that is the ratio of output to input, which is the efficiency of the economic system according to the fundamental science. Microeconomics considers the physical productivity rate of machines and systems that is the number of products fabricated per observation time. Productivity rate is one of the important indicators and criteria for industrial engineering to improve production systems and finish its perfect output [8].
Productivity theory considers the output of machines and systems in terms of the physical productivity rate, i.e., the number of products manufactured per observation time that ASME accepted. Solutions to these problems have represented the progress in developing industrial machines that are manifested in the application of innovative technological processes that enable the increase of their productivity rate. Hence, the perspective designs of manufacturing machines and systems request from engineers and technologists the wide knowledge and prospects and understanding the essence and regularities in developing industrial engineering [9].
Microeconomics is the fundamental component of macroeconomics and each of them has its own indices that reflect thy level of perfectness. The growth of macroeconomics is leading to the growth of the power of the state and the living standard of the population.
Methodology
Macroeconomics studies the state’s economy and the economic decisions of a company or industry. Macroeconomics productivity is a measure of the efficiency of production systems, where the term productivity is a ratio of the output to the input of labour or the amount of output per unit of input (labour, equipment, energy, and capital). There are many indies of economic productivity. Productivity may be conceived of as a metric of the technical or engineering efficiency of production and might be measured by the number of hours spent to produce a product. Economists give a definition of the efficiency of production as the ability to accomplish a job with minimum expenditure of time and effort. In addition, in economics, there are several partial mathematical models and definitions of productivity and efficiency for production systems. With help of the production function, it is possible to describe simply the mechanism of economic growth that presents a production increase achieved by an economic system. Economic growth is evaluated by two relative factors that are preferably a decrease in the production input and an increase in the production output. Both of them can be expressed by financial cost units. These components are represented mathematically by the following typical equation for the labor productivity:
(1)
where L is the labour productivity as the ratio of the numerator of Eq. (1) that presents the output and denominator that is the input of the economic system that is the expenses for production processes; Q is the physical productivity rate of the economic system (products/year); N is the service years for the economic system (factory, plant, industry, etc.); Cf is the fixed capital (cost of buildings, roads, lories, facilities, machinery, power station, computer center, etc.), Cs is the service capital (cost of materials, energy, maintenance, cooling, water supply, etc.), S is the salary of employees.
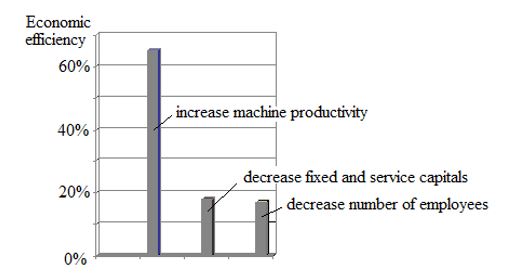
Economists analysed Eq. (1.1) and demonstrated how labor productivity depends on the value of its components and their influence on the economic system. Each component of Eq. (1) has its own weight and presents the following percentage: the machine productivity Q gives 60-70% of economic efficiency (automation and new technology); the fixed capital Cf and the service capital Cs give 15-20% of economic efficiency as the quality of products, and the number of employee’s S gives 10-15% of economic efficiency. Therefore, physical or machine productivity is the main and weighed component of inefficiency of the economic system.
Growth potentials in labour productivity vary greatly by industries, and as a whole, they are directly proportionate to the engineering development in the branch. New and fast-developing industries attain stronger growth in labour productivity. Developed industries demonstrate labour productivity grows in small steps. By the accurate measurement of labour productivity, it is possible to appreciate these small changes and create an organizational culture where continuous improvement is a common value. Today experts understand that human and social capital together with competition has a significant impact on labour productivity growth. Figure 1 depicts the percentage in the average impact of parameters for economic efficiency of production systems, i.e., increase machine productivity, decrease the fixed and service capitals, and decrease the number of employees.
Figure 1: Growth of economic efficiency versus increase machine productivity, decrease fixed and service capitals, and decrease number of employees.
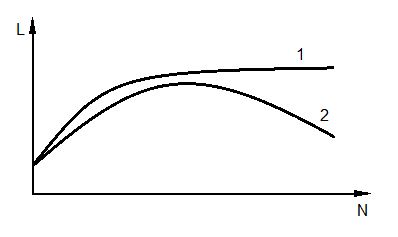
Analysis of Eq. (1) demonstrates the labour productivity is variable with the time of the service of the economic system. It grows intensively at the first years of functioning of the economic system, then the growth is decelerating and monotonically comes to its limit (curve 1). Curve 2 is described below)
Figure 2: The change in the labour productivity vs to the number of years of service of the economic system.
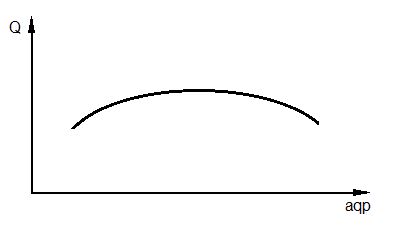
Figure 3: The change in the productivity rate of the automated line of the parallel-serial structure vs to the number of the parallel and serial stations.
The diagram of the change in the labuor productivity clearly demonstrates that any economic system with permanent technology and service has a limit and with the years becomes obsolete and does not respond to the marketing environment. It means the economic system should find ways for constant growth and not to be bankrupt. The answer to this problem is also presented in Eq. (1) and Figure 1. To have a high value of the labour productivity is necessary first of all to develop the new technology with a high productivity rate, then decrees the expenses on the fixed and variable capitals. These are obvious ways to increase the value of labour productivity but the economic system should spend capital to realize them.
Microeconomics studies the economic decisions of an individual firm or groups of firms. Microeconomics is considered mainly the index of the physical productivity rate, in which the term productivity refers to the ratio number of products fabricated per time. Engineering science (ASME) presents the term of productivity as the amount of work that can be accomplished in a given time period. The amount of work is represented as the number of products that can be discrete and continuous for production systems in the form of the number of the products, weights, length, volume, etc., which depends on the type of industries. Dimensions for physical or technical productivity represent as a number of products/time, meter/time, liter or m3/time, kg/time, etc. Differences in productivity measurement models are made transparent and evaluated by clear technical units in productivity theory that can be used by the following economic models of productivity, which is the highest level of economics.
The physical productivity rate of machines and complex systems is an important and multifactor index that depends on the technology of processes, the reliability of mechanisms, machines, and units, and indices of managerial and organizational activities, which definitely affect the output of production systems. All these components can be represented in mathematical models for the productivity of machines and systems. Manufacturers need mathematical models for the productivity rate for different designs and complexity of industrial machines and systems. Such mathematical models should base on the causal links between all parameters that play important role in the development and evaluation of the production systems. In addition, these mathematical models should reflect changes in the production processes. It means mathematical models for the productivity rate of industrial machines and systems are flexible tools that can give the ability in calculating the economic indices of production systems and take the fast decision for micro and macroeconomics policies. Hence, the productivity theory for industrial machines and systems plays the primary role in the efficiency of the economic system.
The object of productivity theory is an analysis of regularities of development for industrial engineering and the definition of causal links and dependencies, and their quantitative and qualitative descriptions. These positions include analysis of factors that affect the productivity rate of industrial machines and systems. Productivity theory contains mathematical models for the quantitative dependency of the productivity rates of industrial machines and systems on their design, structural and exploitation parameters, and their reliability. Qualitative indices of products are the subject of technology theory that is considered by the productivity theory from point of view to increase the productivity rates of machines and systems. Analytical approaches for the productivity rates enable solving optimally these problems based on the criterion of the high or necessary productivity rate for industrial machines. For the example the functional mathematical model for the productivity rate Q of the automated line of the complex structure with parallel and serial stations is presented by the following equation:
(2)
where the numerator presents the number of the product fabricated and the denominator presents the time spent on the production of them; p is the number of parallel-serial lines; z is the number of the products fabricated per observation time; tm is the machining time of the products; a is the coefficient of the intensification of the machining regime; q is the number of the serial stations; ta is the auxiliary time spends on a load of the work part into machining acre, fixing and clamping it and back; ti is the idle time of the automated line due to reliability problems; tmg is the idle time due to managerial problems that linked with the discipline of technicians and workers servicing the automated line, absence of the work parts for machining and control instrumentations, drop of the power; etc.
Analysis of Eq. (2) demonstrates the productivity rate is variable and depends on the number of the parallel and serial stations and other components. The functional dependency of each component is readable at Eq. (2) The diagram demonstrates the growth with incising of the number of stations at the beginning, reaches the maximal value, and drops down (Fig. 3).
Equation (2) has detailed mathematical expression with indices of theological process, reliability of units, design parameters, and indices of the management. Equation (2) enables analytically defining the optimal structure of the automated line and regime of machining by the criterion of the maximal productivity rate. Production systems of industries use different manufacturing machines and systems with complex structures. All of them have their own mathematical models for the productivity rates that enable computing them at the project and design stages and at the conditions of the real production environment. All mathematical models for the productivity rates of the industrial machinery are presented in the fundamental book [9]. This book is a powerful tool for engineers and practitioners.
Two mathematical models (Eqs. (1) and (2)) enable to solve analytically the complex problem of the optimal time of exploitation of the production machinery by the criterion of the maximal labour productivity. For example, substituting Eq. (2) into Eq. (1) that contains the symbol Q yields the new equation that has the following expression:
(3)
where all components are as specified above.
The diagram of Eq. (3) will have three axes that present the variables N, p, q and a that enable defining the optimal structure of the automated line, regimes of machining and optimal years of its exploitation. The change in the labour productivity vs of the time and technical parameters of the economic system is presented by the curve 2 of the Figure 2. This diagram can be computed and presented graphically by the software MathCAD and MathLab. The derived method enables analytically solving the engineering and economic problem clear and predictable and avoid any wrong computing.
Discussion
Proposed productivity theory for industrial engineering collected all achievements in analytical and practical experience in formulation the physical productivity for different manufacturing systems with simple and complex designs. Productivity theory for industrial engineering discovers laws and causal links for creating manufacturing machines and complex production systems. It is necessary to point this productivity theory is universal and can be applied to any type of industry, i.e. manufacturing, textile, transport, chemical, etc. because the mathematical models are universal which symbols and expressions can reflect the specificity of each industry [9].
The basic attributes of any industrial machine and system are productivity rate and quality of products. Attributes of productivity are basically related to the theory of technological processes, the theory of machine design, the theory of reliability, the theory of optimizations, the theory of management, theory of economics, let alone the theory of efficiency of machines. Productivity theory presents mathematical models of productivity rate for machines and manufacturing systems and demonstrates the links between physical productivity rate, reliability, technological and technical parameters, the structure of machines and systems with complex designs, and manufacturing management.
Productivity theory considers all factors that influence the output and design of manufacturing machines and systems. The first factor is the technological processes that are the essence of design for any manufacturing machines and systems, which define the limits of the productivity rate and time spends for the production process. Other theories that applied to the design of manufacturing machines and systems enable decreasing the nonproductive or auxiliary and idle times of production processes. The objective of the productivity theory is to provide the methods and mathematical models for study the regularities and reasonable links in the design of manufacturing machines and systems with optimal structures and the maximal productivity rate.
The contemporary industrial machines and systems are considered systems that contain different mechanisms and arrangements and represent a conglomerate of mechanical, electrical, and electronic units. The structures of manufacturing machines and systems are also having large variances with the serial, parallel, and mixed location of machines arranged according to the technological process for machining products. Any failure of components leads to downtime of expensive production systems that should be minimized by different solutions.
Most of the known publications present the mathematical models for the productivity rate of machines and systems based on the simplifications, which enable deriving approximate equations for productivity rate. These approximate approaches give analytical solutions for the productivity rate of the manufacturing systems and result in the calculation of technical data that far from the real output of machines. Manufacturers need correct and clear mathematical models that enable computing with high accuracy the productivity rate of the machines and systems. This is an important position that enables predicting on preliminary stages the design and output of new manufacturing machinery and systems. The mathematical models of productivity theory allow for the productivity rate of manufacturing machines and systems to be described with results that respond to their actual output. This holistic universal productivity theory presents in the book R. Usubamatov, Productivity theory for industrial engineering, Tylor & Francis, 2018.
Conclusion
The productivity theory presents the analytical approaches and methods to define productivity rate for the manufacturing machines and systems based on parameters of technological processes, reliability of mechanisms and units with different failure rates, and management systems. In addition, this theory enables demonstrating the productivity losses and their reason in real production environments. Such universality of productivity theory for solutions of productivity problems for manufacturing machines and systems can be used by complex and purposeful approaches for sustainable improvement of the production process. The productivity theory enables accurate solving of the problems of designing the machines and systems based on innovative technologies with high manufacturing productivity rates. Productivity theory enables defining optimal balancing technological processes, optimal machining regimes, and optimal structures of manufacturing machines and systems by the criterion of necessary or maximal productivity rate and sustainable improvement of the production process. Productivity theory for industrial engineering is a core course for manufacturing and industrial engineering departments and faculties of universities and should be a desk book for practitioners and manufacturers.
References
- Chryssolouris G. Manufacturing systems: Theory and practice. 2nd ed, New York: Springer; 2006.
- Groover M P, 2013 Fundamentals of Modern Manufacturing: Materials, Processes, and Systems. 5th ed, John Wiley & Sons; 2013.
- Kalpakjian S, Schmid SR. Manufacturing Engineering & Technology. 7th ed. Pearson: Cambridge; UK: 2013
- Koenig DT, Manufacturing Engineering: Principles for Optimization. 3rd ed. ASME; 2007: 1-30.
- Mehta BR, Reddy JY. Industrial Process Automation Systems, Butterworth-Heinemann. 1st ed. Elsevier: USA; 2014.
- Rao RV. Advanced Modelling and Optimization of Manufacturing Processes. 1st ed. Springer Series in Advanced Manufacturing: 2011.
- Schey J. Introduction to Manufacturing Processes. 3 ed. McGraw Hill Education. New York: USA; 2012.
- Thompson R. Manufacturing Processes for Design Professionals, Thames & Hudson. London; UK: 2007.
- Usubamatov R. Productivity theory for industrial engineering, Tylor & Francis. New York; London: 2018.